The simulated annealing (SA) algorithm is a heuristic method that identifies the global optimum for an optimization problem (e.g. traveling salesman problem, mate allocation or group allocation ). The method excels when a solution that is near the global optimum is acceptable, but may not the precise optimal solution. It is well suited for problems that become intractable when all possible solutions are unumerated, often refered to as "combinatorial explosion". Simulated annealing is designed to mimic the process of heating an object to its 'annealing' temperature and once reached the temperature is slowly cooled to alter the object to the desired structure. An object that is near its annealing temperature is more susceptible to change and as the temperature cools less change occurs. The idea of slow cooling in SA is, as the temperture decrease the probablility of accepting a worse solutions decreases. Accepting a worse solution when the temperature is high allows for a more extensive search for the global optimal solution. This can be seen as the explore vs exploitation trade-off. Early on when many iterations remain it allows for more 'explorative' changes to occur while when few iterations remain its 'exploits' the current area to find optimal solution. This is one of the first optimization methods I learned and its ease of coding to any type of problem is big bonus. The code below is the general flow of how to code simulated annealing (when trying to minimize cost) and the associated R code shows multiple different uses for simulated annealing. The primary thing that needs to be adjusted is the step size, which controls the rate at which the temperature drops. The step size is also related to the number of iterations the program is set to run also. When a new solution is generated this can be thought of as exchanging two dam/sire mate combinations, generate a single new pen combination, etc. This aspect is what makes it very flexible and can be utilized across a variety of situations.
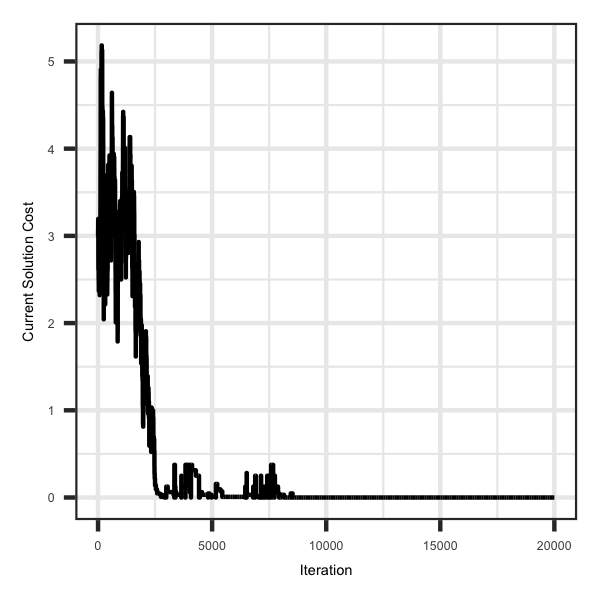
Background on this example is that you have 's' sires that need to be mated to a total of 'd' dams. Each sire has the same number of matings (e.g. d/s). The goal is to minimize the expected pedigree based inbreeding in the progeny. The figure below is the cost, which in this case is the sum of the expected inbreeding in the resulting progeny, across iterations. As can be seen the best possible solution was found (e.g. mating of individuals that are unrelated based on pedigree information).
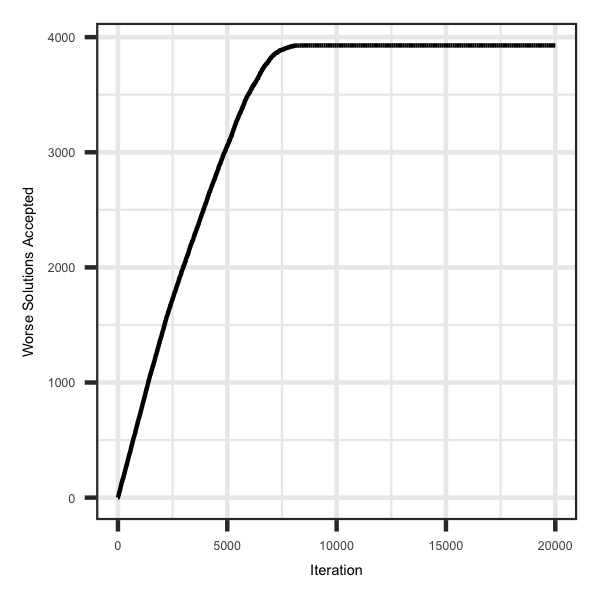
The figure below is the total number of solutions that were accepted that were worse than the current solution across iterations number and illustrates how worse solutions are selected at the beginning and after 6,000 only better solutions are accepted.
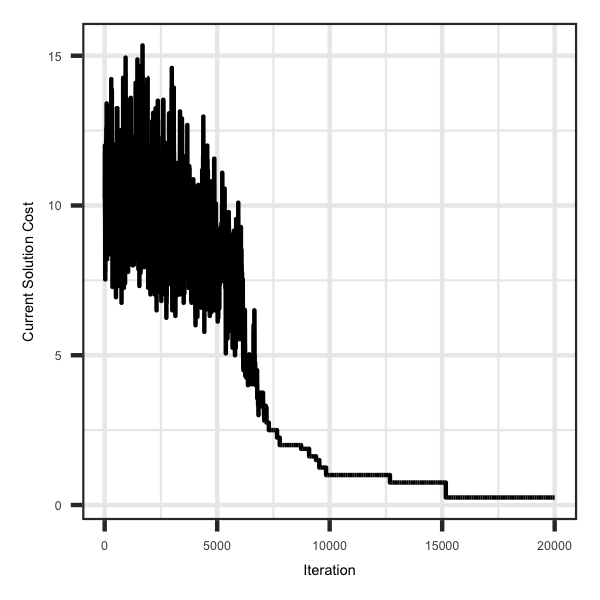
Background on this example is that you have a total of 'p' pens that need to be filled with a total of 'n' animals. An animal can only be allocated to one pen. The goal is to minimize the relationships within a pen so as to not confound genetic relatioships with the effect of the pen. In this case we assumed 10 pens with 10 animals per pen and the simulation was 10 sires with 100 females. So the optimal solution should be 0, but depending on the seed you use you may reach it or you may not. In this case I got really close, which if you wanted the program you would just need to just adjust the number of iterations and step size.
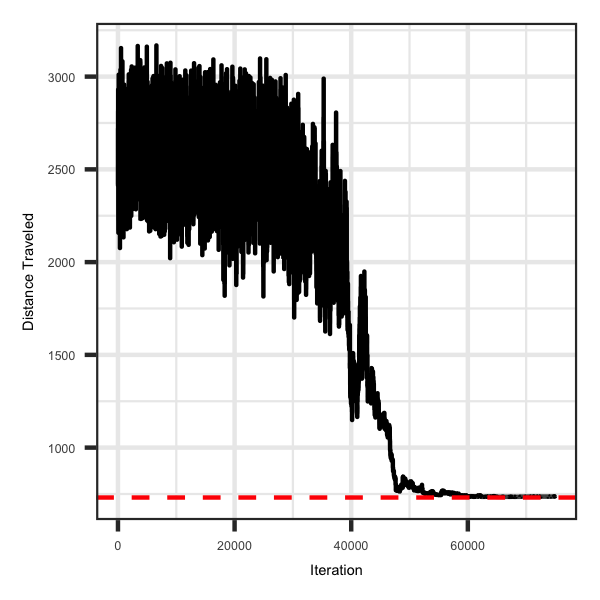
Finding the optimal solution for the 'The Traveling Salesman' problem is a like a rite of passage that I just had to include!! The background on this example is to answer the following question, "Based on a list of pre-defined cities you want to travel too and the distance between each city, what is the shortest possible route that visits each city exactly once and returns to the origin?". I used the Djibouti dataset found here, which has a known optimal solution, which I believe is 731 km. The dashed line in the plot below depicts the optimal solution.